o than states a law Bernoulli (here
h -a depth under the surface of water v - velocity, W - a heat function units of volume )
follows that in this spot 0: B=(W - gh)
W = P /
current lines:
1. Bases models.
A Main thesis:
Near Bottom of vapour-gas channel inheres spot of zero velocity hydrodynamic
motion - a spot 0. (Pic.1-4)
An Effect of thesis:
1)From constancies on current lines of a value ![]() =B,
=B,
o than states a law Bernoulli (here ![]() - density of liquid, g -constant free
falling,
- density of liquid, g -constant free
falling,
h -a depth under the
surface of water v - velocity,
W - a heat function units of volume )
follows that in this spot 0: B=(W
- gh)![]() . If consider a
motion an isoentropy,
. If consider a
motion an isoentropy,
W = P /![]() , where P -a pressure of liquid, and then,
as far as pass near spots 0
, where P -a pressure of liquid, and then,
as far as pass near spots 0
current lines:
a) go out on surface of liquid and
b) with small velocity (nearly surfaces of current line
have a rarefaction),possible
take : ![]() (1)
(1)
where P - an
atmospheric pressure, h - a depth of channel,
close depth of flooding a spot
0 - a zero velocity of moving a liquid, P
- a pressure of liquid just subon the bottom
of channel.
Consequence: ![]() (1" )
(1" )
2 Since experimental values h = 1cm , this
signifies that
process of evaporation in vapour-gas channel occurs
under the atmospheric pressure
practically. Really, condition of the balance position
of bottom of channel in rough
drawing near is defined by equality near it
pressures in fluid phase ![]() and in gas phase
and in gas phase ![]() pressure pair on the day of
pressure pair on the day of
channel. Then swing of pressures between
bottom of channel and atmosphere
![]() pproximately
is -
pproximately
is - ![]() g h , but its relative value:
g h , but its relative value:
![]()
An Equation on the depth of channel.
Position of bottom of channel will
be assign by the condition of balance of power on
the part of liquids and on the part of the gas.
In this balance necessary to take into
account:
a)presssure,
b)form borders of section,
c)variation of density of flow of pulse through the border of section(Pic.4).
a)Pressure.
On first effect from main thesis models a pressure
on the part of liquids
![]()
Pressure a pair on bottom of channel will be assign
by temperature
liquids on the border:
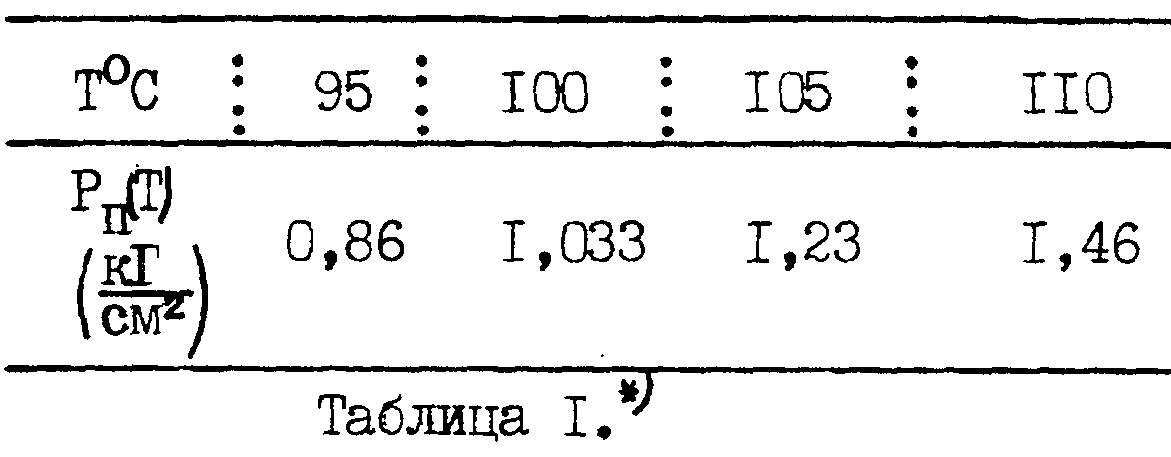
Here ![]() - a pressure saturated pair at the temperature T.
For evaluations near 100°C with
follows to use a correlation:
- a pressure saturated pair at the temperature T.
For evaluations near 100°C with
follows to use a correlation:
![]() (2)
(2)
where ST- an
overheat on the border a liquid - a vapour(Pic4).
b) A form of borders of section.
As is well known , border of section
in form of half-spheres creates additional pressure inwardly![]() ,
where
,
where ![]() - a factor
shallow stretching borders (
- a factor
shallow stretching borders ( ![]() = 58 Din\cm under T=100°C) , R
- a radius of half-sphere(Pic.4).
= 58 Din\cm under T=100°C) , R
- a radius of half-sphere(Pic.4).
c)Variation of flow of pulse under phase transition.
Density of flow of pulse is J´V,
where J - a flow of mass with units of area
J = q´V
,( q - density,
V - a velocity).
As far as under phase transition a mass is not
changed -![]() ,i.e.
mass flows of liquid reduce co to the bottom a channel and pair in the
most channel near bottom alike. Changing density of flow of pulse , answer
pressure of return vaporize pair, will form
,i.e.
mass flows of liquid reduce co to the bottom a channel and pair in the
most channel near bottom alike. Changing density of flow of pulse , answer
pressure of return vaporize pair, will form
![]()
where ![]() - density saturated water pair,
- density saturated water pair, ![]() -
its velocity on day channel,
-
its velocity on day channel, ![]() - density of
- density of
water, ![]() -
a velocity of supply of liquid co to the bottom.
-
a velocity of supply of liquid co to the bottom.
Value density saturated water pair
under atmospheric pressure From equation of condition a pair, considered
as ideal gas,![]() ,
where m - a mass of molecule of water,
k - constant of Bolzman, T
- a temperature.
,
where m - a mass of molecule of water,
k - constant of Bolzman, T
- a temperature.
That gives:
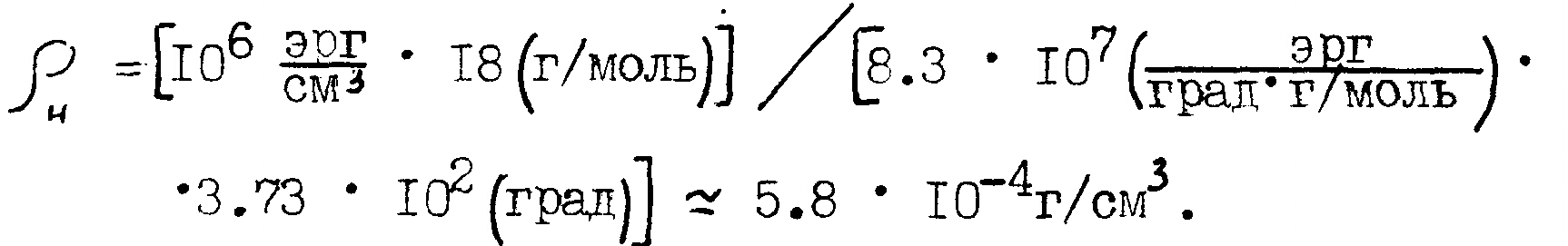
![]()
Tables and the numerical values take from reference books.
Underlining by the wavy line means (indicates) statement,
which are to be more carefully motivated in purposes
of evaluation of borders of aplicability.
![]()